怎样才能学会因式分解?
作为整式变形主要内容的因式分解是解决多项式问题的重要手段.那么如何才能学好因式分解这部分内容呢?笔者以为应注意掌握以下几个问题: 一、正确理解因式分解的意义 把一个多项式化成几个整式的积的形式,叫做把这个多项式分解因式. 由此,我们理解因式分解的这一定义应注意以下几点:一是分解因式的结果是几个整式积的形式;二是分解因式的过程是多项式的恒等变形,即等式左边为多项式,右边是几个整式积的形式;三是等式的右边每个因式必须为整式且每个因式的次数都低于原来的多项式的次数;四是分解因式必须分解到右边的每个因式不能再分解为止. 二、知道因式分解与整式乘法的区别与联系 分解因式与整式乘法是两个互逆变形过程.整式乘法是把几个整式相乘化成一个多项式,结果是单项式的和;而因式分解是把一个多项式化为几个整式积的形式,结果是乘积的形式. 三、掌握提取公因式法分解因式的基本 *** 提公因式法的定义:如果一个多项式的各项含有公因式,那么就把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的 *** 叫提公因式法.提公因式法的理论依据是乘法的分配律,其实质是乘法的分配律的"逆用".公因式的定义:多项式各项都含有的相同因式叫做这个多项式的公因式. 确定公因式的 *** :确定一个多项式的公因式时,需对数字系数和字母分别进行考虑.即①对于系数:如果各项系数都是整数时,取各项系数的最大公约数作为公因式的系数;②对于字母:取各项相同的字母;③对于字母指数:取各相同字母的指数取其次数最低的.
什么是分解因式?
把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也就是把这个多项式分解因式。
1.判断是否为因式分解,先看等式右边是否是乘积的形式; 2.因式分解常用的 *** 有提取公因式,十字相乘,公式法等.
分解因式是将一个多项式分解成其因子的乘积。简单来说,就是将一个多项式表示为一些更简单的多项式的乘积。分解因式在代数学、数论和其他数学领域中都有广泛的应用。
多项式的因子可以是整数、有理数、实数、复数等。常见的因式分解 *** 包括:
1. 用代数公式分解:例如,完全平方公式、平方差公式、立方公式等。
2. 用因式定理分解:例如,分解二次和三次多项式时,可以使用求根公式或因式定理。
3. 用其他 *** 分解:例如,使用长除法、辗转相除法、分组分解法、利用因式的对称性分解等。
分解因式的主要目的是简化多项式,使其更容易理解和计算。在解决实际问题时,分解因式有助于我们更好地理解问题的本质,寻找问题的解决方案。
把一个多项式化为几个最简整式的乘积的形式,这种变形叫做把这个因式分解(也叫作分解因式)。它是中学数学中最重要的恒等变形之一,它被广泛地应用于初等数学之中,是我们解决许多数学问题的有力工具。因式分解 *** 灵活,技巧性强,学习这些 *** 与技巧,不仅是掌握因式分解内容所必需的,而且对于培养学生的解题技能,发展学生的思维能力,都有着十分独特的作用。
因式分解的四种 *** ?
步骤/方式1
一,提公因式法(提)
观察式子中各项是否有公因式,如果有就先提公因式,比如:
例1:

步骤/方式2
二、公式法(套)
公式法说白了,就是套公式,一般来讲,主要是套下面的三个基本公式 ,当然还有立方和、立方差公式等,暂时不作讨论。
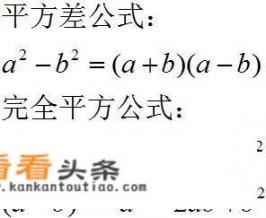
步骤/方式3
三、分组分解法(分组)
简而言之,就是将多项式分成二或三组,分别分解,再提取公因式,当一个多项式不能套用公式且项数比较多时,可以考虑分组分解法。如
例2:

步骤/方式4
四、十字相乘法(交叉)
分式因式分解的 *** 与技巧?
分式因式分解是将一个分式化为几个分式相乘或相除的形式的过程。下面是分式因式分解的一些 *** 和技巧:
1. 查找公因式:可以首先查看分子和分母,看是否存在一个共同的因子,然后将其约掉。
2. 套用公式:对于一些特定类型的分式,可以套用公式进行因式分解,比如平方差公式、立方差公式等。
3. 分离系数:如果分式中含有多项式,可以尝试将其中的系数与单项式分开来计算。
4. 分解因式:如果分式中的分子或分母是多项式,可以使用因式分解来简化分式。
5. 代入值:如果分式中含有未知变量,可以将不同的值代入变量,观察分式是否能够被简化。
6. 拆分分式:有时候可以将一个分式拆分成两个分式之和或之差的形式,这样更容易进行因式分解。
7. 观察规律:有些分式因式分解需要通过观察规律来进行处理,这需要对数学知识有深入的理解和积累。
以上是分式因式分解的一些 *** 和技巧,需要根据具体情况选择合适的 *** 来解决问题。
