指数函数的定义和性质？

指数函数的定义和性质？

指数函数及其性质

（1）指数函数：1般地，函数y=a^x(a>0，且a≠1)喊做指数函数，其中x是自变量，函数的定义域是 R （实数）。”

理解：【1】a^x系数为1，否则不是指数函数；【2】x须在指数位置，且不能是x的其它表达式（即只能是x本身）；【3】a是常数，【4】(为什么要a>0)，如果a=0,指数x≠0时函数值等于0,x=0时函数值无意义，此时自变量就不能取0了。如果a<0,那么a的x次方这个幂将不连续，且出现无法确定是否有意义的不定点。因为负数不能开偶数次方，所以当x是最简分数时，分母为偶数的指数将使得a的x次方无意义。综上：为了指数取值领域为实数所以规定a>0。【5】（a≠1）如果a=1,则y恒等于1,那么这个函数就变成了y=1常数函数，没必要在指数函数中进行研究。

简记：【1】自变量为指数，【2】系数为1，【3】底数为常数，【4】大于零不等于1。

（2）函数的图像和性质：

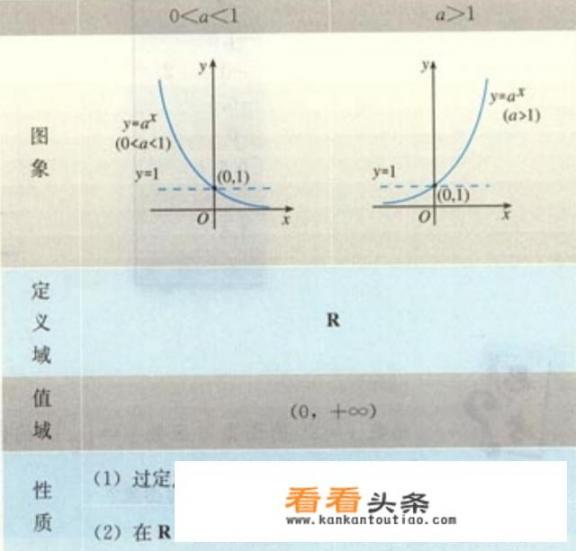
理解：【1】过点（0，1），因为a^0=1(它为什么等于1呢，因为a^(1-1)=a/a=1)，【2】0<a<1,在定义域R（实数）上是减函数；当x>0时，小于1的数自乘次数越多越小；当x<0时，小于1的数自乘次数越多越小，但是取倒数后就变大了。【3】a>1，在定义域R（实数）上是增函数；当x>0时，大于1的数自乘次数越多越大；当x<0时，大于1的数自乘次数越多越大，但取倒数后就变小了。

简记：【1】过点（0，1），【2】a比1小减（函数），a比1大增（函数）。