对数函数图像及性质总结？

对数函数图像及性质总结？

对数函数的一般形式为

，它实际上就是指数函数的反函数。因此指数函数里对于a的规定，同样适用于对数函数。

对于不同大小a所表示的函数图形：

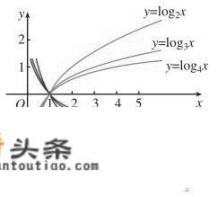
可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形，因为它们互为反函数。

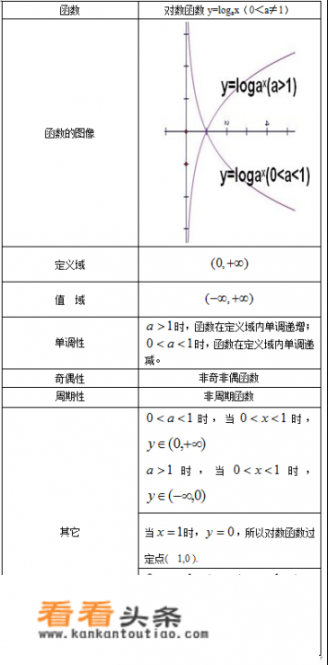
（1）对数函数的定义域为大于0的实数集合。

（2）对数函数的值域为全部实数集合。

（3）函数总是通过（1，0）这点。

（4）a大于1时，为单调递增函数，并且上凸；a小于1大于0时，函数为单调递减函数，并且下凹。

（5）显然对数函数无界。

性质：定义域求对数函数y=loga x 的定义域是｛x ｜x>0｝,但如果遇到对数型复合函数的定义域的求解,除了要注意真数大于0以外,还应注意底数大于0且不等于1,如求函数y=logx（2x-1）的定义域,需满足｛x>0且x≠1｝ .

 ｛2x-1>0 =〉x>1/2且x≠1,即其定义域为 ｛x ｜x>1/2且x≠1｝值域：实数集R

 定点：函数图像恒过定点（1,0）.

 单调性：a>1时,在定义域上为单调增函数,并且上凸；

 0<a<1时,在定义域上为单调减函数,并且下凹.

 奇偶性：非奇非偶函数,或者称没有奇偶性.

 周期性：不是周期函数

 零点：x=1

 注意：负数和0没有对数.